 |
 |
Capital as a factor of production is somestime referred to as an intermediate good that is, a good that is used to produce other (final) goods. In a world of scarcity, resources for the creation of capital must be reallocated away from the production of these final goods. Stated differently, deferring current consumption of final goods frees up resources in the form of savings to be used in the production of capital or intermediate goods. Economic agents can use there resources either for consumption or savings, the the latter represents the Supply of loanable funds -- funds transferred in financial markets to meet the Demand for loanable funds or investment to provide resources for the production of capital goods.
We model decisions to save based on individual preferences for consumption in the present time period and in the future.
Models of individual consumption behavior begin with the notion of an individual maximizing his or her level of satisfaction (utility) from present consumption Co and from future consumption Cf:
max U = f(Co, Cf)
= U(Co) + Σ LU(Ct)(1+ ρ )-t
Into the future this utility from consumption is discounted at some rate 'ρ' the rate of time preference for a given individual. Higher values for this rate imply less satisfaction from future consumption relative to current consumption spending.
This consumption pattern is constrained by current and (expected) future levels of income Yo & E[Yf.]. In this model, the expectation of future levels of income are based on individual skills and talents, and ownership of income producing assets Wo. In addition, consumption patterns are constrained by the prevailing real interest rate 'r' which represents a payment (or reward) for foregoing current consumption.
The two- period model is developed as follows:
max U = f(Co, Cf)
subject to [Yp - Co](1 + r) + Wo = Cf - Yf
Current Savings '[Yp - Co]' multiplied by an interest rate factor '(1+r)' will allow for future consumption in excess of future income. Solving for future consumption as a function of current consumption allows us to write the constraint in intercept-slope form as:
Cf = {Yp(1 + r) + E[Yf] + Wo } - (1 + r)Co
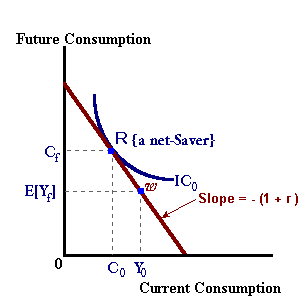
In the diagram below, the curves ICo and IC1represents levels of satisfaction (or utility) received from combinations of present and future consumption activity. Each point on a given curve, known as an indifference curve, represents equal levels of satisfaction from different combinations of consumption in the present and future. The position of an indifference curve (above or below point 'ω' -- the endowment point) depends on the individual's own rate of time preference 'ρ'. The constraint or budget line, in the diagram below, represents the possible levels of consumption in the two periods given the individual's level of present income, future expected income and the prevailing interest rate 'r'. This budget line has a slope equal to -(1 + r) and must pass through point 'ω' denoting the fact that if current consumption equals current income then future consumption and income must also be equal.
 |
 |
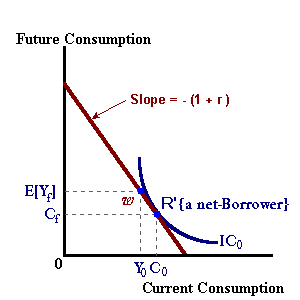
The solid indifference curve ICo represents the behavior of a net-saver (an individual with strong preferences for future consumption relative to current consumption) in the current time period -- current income exceeds current consumption. For this individual, these savings along with an interest payment may be used for future consumption in excess of future income. The dashed indifference curve IC1 represents the behavior of a net-borrower (an individual with strong preferences for current consumption). Funds are borrowed from the future at an interest rate 'r' to allow for current consumption to exceed current income.
As in all indifference curve models, a tangency between an indifference curve and the budget line represents an equilibrium position for the individual. Within the two-period consumption model, it is interesting to look at the effect of changes in the interest rate and future expected income on consumption patterns and on savings or borrowing activity.
An increase in the interest rate will cause a clockwise rotation in the budget line as shown in the next diagram. This increase makes savers better off (they will be on a higher indifference curve) and borrowers worse off. When the interest rate increases, current consumption becomes relatively more expensive (the interest rate represents the "price" of current consumption) thus the individual will tend to substitute away from current consumption. This movement is known as the substitution effect. However, assuming that present and future consumption are both normal goods, an increase in the interest rate will increase relative income leading to what is known as the income effect. For a net-saver this increase in relative income will thus induce him to "buy" more current consumption.
With a strong substitution effect (relative to the income effect), we can expect that the individual will react to an increase in the interest rate by saving more -- current consumption has become relatively more expensive. With a stronger income effecgt, we might find that the individual saves less with an interest rate increase. In this case, the individual is buying more current and future consumption with interest income earned. In summary, we note that the relative sizes of substitution and income effect can affect the responsiveness (weaker / stronger) of savings, and the availability of resources lent to financial markets, with changes in interest rates.
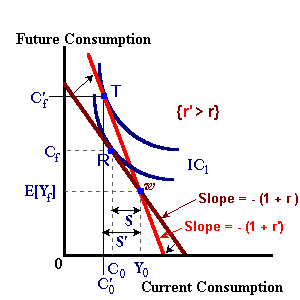
The opposite is true for the borrower where the reduction in relative income leads to the "purchase" of less consumption in the present time period. Therefore, the income effect will be positive for a net- saver and be negative for the net-borrower in contrast to the substitution effect which is negative for both types of individuals. The substitution and income effects work in opposite directions for the net- saver. Therefore, the effect of changes in the interest rate on savings behavior depends on the relative size of the two effects. If the income effect is greater than the substitution effect (i.e., the individual has a strong reaction to the increase in purchasing power), then an increase in the interest rate will lead to an increase in current consumption and a reduction in savings. If the income effect is less than the substitution effect (the individual reacts strongly to an increase in the price of current consumption), the opposite will be true. For a net borrower, the two effects complement each other. An increase in the interest rate will always lead to a reduction in present consumption as borrowing from the future become more expensive.
Changes in current income or expected future income can also affect consumption activity in the two time periods. For example suppose that current income is expected to increase perhaps due to an inheritance. This can be shown in a repositioning of the endowment point 'ω' directly to the right of its initial position in the next diagram. This change in expected income might induce the individual to change her or his consumption pattern over the two periods. This individual might desire to use some of this increase in expected income to allow for increases in both current and future consumption. In a similar manner an expected increase in future income (the endowment point shifts straight up) cold also lead to greater levels of present and future consumption expenditure. It is important to note that in this example expectations about the future have a direct and real impact on current economic activity through changes in consumption behavior.
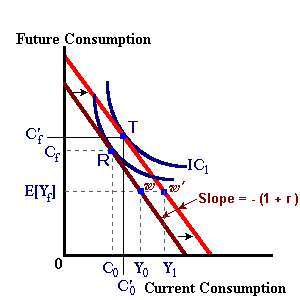
The impact of changes in income taxes may be examined as well. However the reaction of the individual depends on how these tax changes are perceived. If, a tax cut in the current time period is deemed permanent by the individual (such that taxes will not be adjusted upwards at some point in the future) he will react with the expectation that current disposable income will be greater and thus alter his consumption plans (an outward shift in the budget constraint ω to ω'
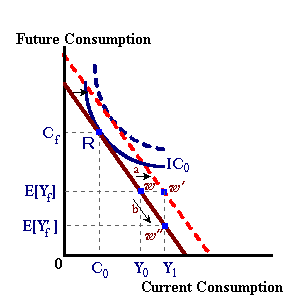
If, however, the tax cut is deemed transitory (the individual realizes that tax cuts lead to budget deficits in the future -- deficits that must be financed with future tax increases), he will use the tax cut to save for the expected future tax increase. The result is a movement of the endowment point along the budget constraint (ω -greaterthan; ω') with no corresponding change in consumption spending.
|
|