In describing a short run producer optimum for an individual firm, we have defined the profit maximization condition with respect to the variable factor input (labor) as:
MPL = w/P.
or
P = w/MPL = MC.
If we step forward to the market for goods and services For the competitive firm (a price taker), we can note that :
Sales (Total) Revenue (TR) = Pmkt x Q
The price Pmkt is determined by competition in the market and taken as a given by the individual form (a.k.a. a price-taker). Thus, additional revenue earned by selling one more unit (Marginal Revenue) is exactly equal to this price.
Marginal Revenue (MR) = dTR/dQ = Pmkt
This provides an alternative expression for profit maximization for a competitive firm as:
MR = MC.

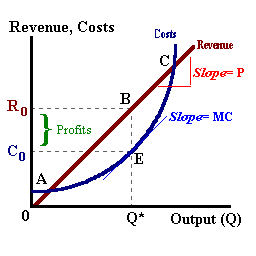
A profit-maximizing level of output can be described as where the revenue from selling one more unit of output (P or MR) is exactly equal to the cost of producing that last unit of output (MC).
If, at a given level of production P (MR) > MC then the addition to revenue exceeds the addition to cost by producing and selling one more unit of output and the firm will be able to increase profits by selling that additional unit.
If the opposite is true, P (MR) < MC then additions to costs exceed the additions to revenue (via the production and sale of one more unit of output) and the firm will be able to increase profits by reducing output by one unit.
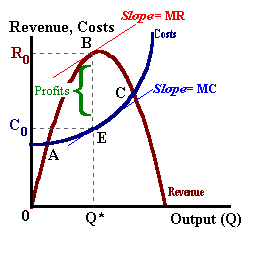
In the case of a firm in the market with a certain degree of pricing (monopoly) power -- a price maker, the market demand curve is also the demand curve for that firm's output. Assuming that the demand curve is linear we find:
P = a - bQ -- the inverse demand curve
and
TR = PxQ = aQ - bQ2 -- Total Revenue -- a quadratic equation!
and
Marginal Revenue (MR) = dTR/dQ = a - 2bQ
The equation for Marginal Revenue has the same intercept 'a' and is twice as steep as the slope of inverse demand. The condition for profit maximization still holds:
MR = MC.
 |
 |
If the level of output is below Q*, MR > MC, additional units sold will generate more additional revenue as compared to the additional costs of producing those addtional units. This firm will induce the addional sales by lowering the price charged. Increasing production and units-sold will lead to higher profits.
If the level of output is above Q*, MR < MC, additional units sold will generate less additional revenue as compared to the additional costs of producing those addtional units. This firm will reduce sales by raising the price charged. Decreasing production and units-sold will lead to higher profits.
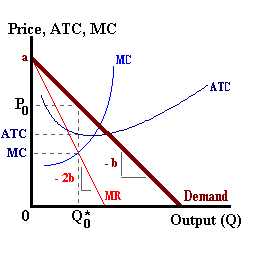
In the real world, a firm with pricing power may raise and lower prices via trial an error, keeping track of profitability. The target price charged (P0 in the right diagram above) will be consistent with the profit maximizing condition of MR = MC.
|
|