Price Elasticity is a numeric measure that helps managers, policy makers and analysts understand market sensitivity of changes in price. It is a unit-free measure calculated by the ratio of the percentage change in quantity demanded for a given percentage change in market price.
ηp = %ΔQD / %ΔP
For example, if the value of η is equal to -4.0, we could calculate:
%ΔQD = ηp x %ΔP
or
%ΔQD = -4.0p x %ΔP
with the interpretation that a 1% change (increase) in market price will lead to a 4% change (decrease) in quantity demanded. Managers might use this type of calculation for production planning based on expectations of changes in the market price of their product.
An important characteristic of demand is the relationship among market price, quantity demand and consumer expenditure. The nature of demand is such that a reduction in market price will usually lead to an increase in quantity demanded. Given that consumer expenditure is the product of these two variables, the effect of a price reduction will have an uncertain impact on this expenditure. In some cases a reduction in price will be more than offset by a large increase in quantity demanded -- a situation where demand is price sensitive or price elastic.
(Pmkt↓) (Qdemanded↑) = Expenditure↑
In other cases, the reduction in price results in a proportionally smaller increase in quantity demanded-- a situation where demand is price insensitive or price inelastic.
(Pmkt↓) (Qdemanded↑) = Expenditure↓
Note that the concept of consumer Expenditure (Pmkt x QD) is the equivalent of Total Revenue received by the business firm.
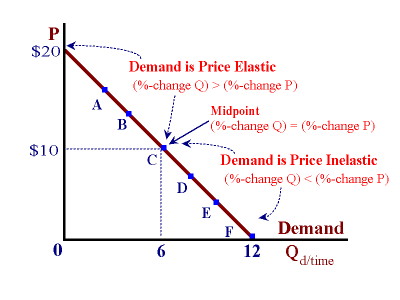
This relationship between price and quantity (for a linear demand function) can demonstrated in the diagram below:

When the price falls from $16 to $14 -- a 12.5% reduction, quantity demanded increases by 100% (2 units to 4 units). Thus
%ΔQd > %ΔPmkt
and Expenditure increases. Note that at point A consumer expenditure is equal to ($16 x 2) $32.00. At point B expediture is equal to ($14 x 4) $56.00.
However, when the price falls from $6 to $4 (a 33.3% reduction -- same $2 price change with a smaller base number), quantity demanded only increases by 12.5% -- from 8 to 10 units and expenditure falls.
On a linear demand function, all points on the upper half of the functionrepresent price-quantity combinations where demand is price elastic. Points on the lower half represent combinations where demand is price inelastic.
At the midpoint, %ΔQD == ΔP, and demand is defined to be Unit Elastic -- revenue is a maximum at this point. Also note that at a price of zero (the horizontal intercept), the price elasticity of demand is equal to zero.
Given the ratio: %ΔQD / %Δ P:
if (%ΔQ) > %(ΔP) then |ηp| > 1.0 and demand is price elastic
if the opposite is true then:
|ηp| < 1.0 and demand is price inelastic
This relationship between price changes and expenditure can be summarized in the following table:
| Elasticity | Demand is Price Elastic: |hp| > 1.0 |
Demand is Price Inelastic: |hp| < 1.0 |
| a Price Reduction | Expenditure increases | Expenditure decreases |
| a Price Increase | Expenditure decreases | Expenditure increases |

Public Transportation As noted above, a price elasticity calculation is a useful metric to support various types of decision making. For example, public transit agencies will from time to time temporily lower their structure of fares. This provides an second data point -- a second price (fare) - quantity (ridership) to evaluate the effect on total revenue. These transit agencies differ from purely private business firms in that some of their costs are covered by special tax jurisdictions. The combination of tax revenue and fare revenue is used to cover costs of operation.
If the transit agency finds that ridership is price sensitive, they can increase revenue by making the fare reduction permanent. If ridership is fare-insensitive (maybe because of fewer inexpensive transportation alternatives), the agency can increase revenue by raising the fare above the original value.
Production management Production managers can use elasticity calculations to ensure that demand for a product matches production capacity. For example, suppose that the price elasticity of a given product is equal to -1.75. Because of an anticipated market shock, say an increase in consumer income, demand is expected to increase by 7%. But existing production capacity is at its limit. The firm can increase price (provided they have some pricing power) by 4% and mitigate this increase in demand.
-%ΔQD = ηp x +%Δ P
-7% = 1.75 x 4%